Намерете момента на инерция на триъгълника. Геометрични характеристики на плоските участъци

Аксиалният момент на инерция е сумата, взета по целия участък, от произведенията на елементарни площи и квадрата на разстоянието до някаква ос, лежаща в равнината на разглеждания участък. Аксиалният момент на инерция е мярка за способността на лъча да се противопоставя на деформация при огъване.

J - Аксиален момент на инерция

J x \u003d

J y \u003d

Аксиален момент на съпротивлениенаречено отношение аксиален момент инерция към разстоянието до влакната на участъка, най-отдалечен от неутралната ос.

W - Аксиален момент на съпротивление.

W x \u003d, W y \u003d

Полярен момент на инерция се нарича, взета по цялата секция, сумата от произведенията на елементарни площи по квадратите на техните разстояния до центъра на тежестта на сечението. преди пресичането на координатните оси.

Полярният момент на инерция характеризира способността на частта да устои на деформация на усукване.

Полярен момент на инерция.

= .

Полярен момент на съпротивление е съотношението на полярния момент на инерция към разстоянието до най-отдалечените точки на участъка от центъра на тежестта на разглеждания участък.

Полярен момент на съпротивление

1. Правоъгълно сечение.

J y \u003d (mm 4), J x \u003d (mm 4)

W x \u003d (mm 3), W y \u003d (mm 3)

2. Кръгло сечение

J x \u003d J y \u003d (mm 4), \u003d (mm 4)

W y \u003d W x \u003d (mm 3), \u003d (mm 3)

3. Пръстеновидна секция

J x \u003d J y \u003d - \u003d (mm 4), α \u003d d / D

W y \u003d W x \u003d (mm 3)

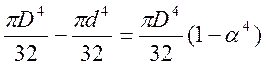= (mm 4)

= (mm 3)

4. Кутийка.

J x \u003d = (mm 4)

J y \u003d = (mm 4)

W x \u003d (mm 3)

W y \u003d (mm 3)

Изчисления на части с равномерно разпределение на напрежението.

Този тип части включват пръти с уши и щифтове, както и хидравлични и пневматични цилиндри и други съдове под налягане, биметални елементи (термични релета).

Изчисление на сцеплението.

1) Сила на опън F, приложена към пръта.

Прътът възприема надлъжно натоварване, под действието на което се разтяга. В този случай величината на абсолютното удължение се определя от разширения закон на Хук:

σ p \u003d Eε. , σ р \u003d F / A, , σ р \u003d F / A<=[ σ р ]= σ T / n -

условие на якост на опън, (A \u003d H * B, A \u003d).

Ушите, в резултат на взаимодействие с пръста, се смачкват върху контактната зона.

Условие на сила на свиване:

σ cm \u003d F / A<=[σ см ]= 2σ T / n , A=d*b.

Пръстите се изчисляват за разрез от взаимодействието с ушите:

τ cf \u003d F / A<=[τ ср ]= 0,5σ T / n; A=*i, i - количество платежей среза (i=2).

2) Към тягата се прилага сила на натиск F2.

Аксиалният прът е в компресия. Размерът на абсолютното съкращаване също се определя от закона на Хук:

σ c \u003d F / A<=[σ с ]=[σ р ]=σ T / n. – Для коротких стержней тяги.

Дълъг прът - когато дължината е 3 пъти една от размерите на напречното сечение. Има възможност за мигновено огъване на тягата.

σ с \u003d<=[σ с ]=[σ р ]=σ T / n, φ – коэффициент продольного изгиба, величина табличная – зависит от материала, гибкости стержня и характера закрепления концов стержня.

Ухото и пръстите се изчисляват подобно на предишното изчисление.

Изчисляване на тънкостенни съдове.

Тънкостенните съдове включват хидравлични и пневматични цилиндри, приемници, тръбопроводи и др.

В зависимост от формата, съдовете са:

цилиндрични (хидравлични и пневматични цилиндри, някои видове приемници, тръбопроводи);

топка (някои видове приемници, дъна и капаци на цилиндрични съдове, мембрани и др.);

торус (извити участъци от тръбопроводи, чувствителни елементи на измервателни уреди).

Във всички съдове под действието на вътрешни сили на течност или газ се появяват напрежения в стените в надлъжното и напречното сечение.

Цилиндрични съдове.

Тънка цилиндрична обвивка е натоварена с вътрешно налягане P. - Изчислено като напречно сечение на цилиндър.

Разкъсани съдове.

Те се изчисляват като извити цилиндрични.

15.10.04 Изчисляване на напреженията, произтичащи от температурни промени.

При температурни колебания част, фиксирана между твърдите опори, изпитва деформация на компресия или опън. С повишаване (намаляване) на температурата с Dt, пръчката трябва да се удължава (съкращава) с размера на абсолютното удължение (скъсяване):

дл= а т* л* дт, където a t е температурният коефициент на линейно разширение (за стомана 12 * 10 -6 ° С -1), тогава величината на абсолютното удължение (скъсяване): Δε t \u003d Δ l t / л = α t* дт, но тъй като прътът е твърдо фиксиран, тогава той не може да се удължава (съкращава), поради което в неговия материал ще възникнат напрежения на натиск (опън), чиито стойности се определят от закона на Хук:

σ с, р \u003d Е * ε t \u003d E * α t * Δt.

В изчислителната практика сеченията често се намират под формата на най-простите фигури (правоъгълници, кръгове, триъгълници и т.н.) или техни комбинации. При изчисляване на моментите на инерция на такива фигури обикновено се използват предварително изведени формули за изчисление. Нека разгледаме някои от формите.

Правоъгълник и успоредник (фиг. 6.4). Нека изберете елементарна лента с площ dF= bdy и заменете тази стойност dF под интегралния знак (6.5):

Моментите на инерция на тези фигури спрямо осите, преминаващи през основата, се намират по формулата (6.13):

Моменти на инерция на правоъгълник около осите у ° С и у се изчисляват по формули (6.16) и (6.17), където б се заменя с з, и з На б:

Изчислявайки момента на инерция на триъгълника около централната ос, успоредна на основата, чрез формулите за прехвърляне получаваме

Обикновено размерите на кръговото сечение се изразяват чрез диаметъра д и пребройте Аз стр според формулата

Централни оси у и z разделете окръжността на четири напълно еднакви части с равни моменти на инерция около тези оси. Следователно инерционните моменти на окръжност и полукръг около осите у и z трябва да бъде равен, съответно, да умножи и удвои моментите на инерция спрямо същите оси на една четвърт от окръжността. От казаното следва, че инерционните моменти на полукръга около оста на симетрия у и брадви z, преминавайки през основата му (фиг. 6.2), ще бъде еднакъв и равен на половината от инерционния момент на окръжността,

и инерционните моменти на четвърт кръг

За прости секции статичните моменти и моментите на инерция се намират от формули (2.1) - (2.4) с помощта на интегриране. Помислете например за изчисляване на аксиалния момент на инерция J x за произволен разрез, показан на фиг. 2.9. Като се има предвид, че в правоъгълна координатна система площният елемент dF \u003d dxdy, вземете

къдетоdex ^ (y) и х в (у) - координатите на точките на контура при някаква фиксирана стойност в.

Интегрирайки над x, намираме

Количеството Б (у) е ширината на участъка на нивото в(виж фигура 2.9) и продукта b (y) dy \u003d dF - площ на сенчестата елементарна ивица, успоредна на оста О Имайки това предвид, формулата за / се преобразува във формата

Подобен израз може да се получи за момента на инерцията J y.

Правоъгълник.Нека намерим моментите на инерция относно основните централни оси, които в съответствие със свойство 2 (§ 2.5) съвпадат с осите на симетрия на правоъгълника (фиг. 2.10). Тъй като ширината на напречното сечение е постоянна, по формула (2.14) получаваме

Момент на инерция около оста О х х х дефинираме с първата от формулите (2.6):

Моменти на инерция / и J се намират по подобен начин. Нека напишем формулите за аксиалните моменти на инерция на правоъгълника:

Произволен триъгълник.Първо, намираме момента на инерция около оста 0 (x v преминавайки през основата на триъгълника (фиг. 2.11). Ширина на участъка B (y () на ниво в ( се намира от сходството на триъгълниците:

Замествайки това количество във формула (2.14) и извършвайки интегриране, получаваме

Моменти спрямо осите О и 0 2 x 2, успоредни на основата и преминаващи съответно през центъра на тежестта и през върха на триъгълника, намираме с помощта на формули (2.6):

В тези формули b (\u003d h /3 и b 2 \u003d -2h / 3 - съответно ординатите на центъра на тежестта на триъгълника ОТНОСНО в координатна система О х х 1 у 1 и 0 2 x 2 y t

1 ° 2 р Г * аУ 1

TL P * 2

r\u003e 4 ™ _ ° 2 1

Д__V _! _ * _ / ^ * 3

V XV *; -7 ^ Am ^

U_ U-_XI - UZ__y

ОТНОСНО,| б *, 0 B / b 2 %*1

Фигура: 2.11 Фигура: 2.12

Нека напишем формулите за аксиалните моменти на инерция на триъгълника около осите, успоредни на основата:

Правоъгълни и равнобедрени триъгълници.За правоъгълен триъгълник (фиг. 2.12) определяме центробежния инерционен момент J за централните оси О и OU, успоредно на краката. Това може да се направи с помощта на формула (2.3). Решаването на проблема обаче може да бъде опростено чрез прилагане на следната техника. Използване на медианата 0 { 0 3 разделете дадения триъгълник на два равнобедрени триъгълника 0 (0 3 A и Ofi 3 B.Оси 0 3 x 3 и 0 3 y 3 са осите на симетрия за тези триъгълници и въз основа на свойство 2 (§ 2.5) ще бъдат основните оси на всяка от тях поотделно и следователно на целия триъгълник О х АБ.Следователно, центробежният инерционен момент J \u003d 0. Центробежен

момент на триъгълника около осите О и OU намираме, използвайки последната от формулите (2.6):

Нека напишем формулите за моментите на инерция на правоъгълен триъгълник:

Моментът на инерция на равнобедрен триъгълник около оста на симетрия OU(Фиг. 2.13) дефинираме, като използваме четвъртата от формулите (2.17), като удвоения момент на инерция на правоъгълен триъгълник с основа з и височина B /2:

По този начин инерционните моменти на равнобедрен триъгълник около основните централни оси О и OU се определят от формулите

Кръг.Отначало е удобно да се изчисли полярният момент на инерция на окръжността по формула (2.4), като се използва полярната координатна система (фиг. 2.14).

Като се има предвид това dF-rdrdQ, намирам

Тъй като полярният момент съгласно (2.4) е равен на сумата от два аксиални момента, получаваме

Пръстен.Моментите на инерция на пръстена (фиг. 2.15) се намират като разлика между моментите на инерция на два кръга с радиуси Аз съм 2 и R (:

Полукръг(фиг. 2.16). Изберете елемента площ в равнината на полукръг dFс полярни координати r, 0 и декартови координати x v y v за които в съответствие с фиг. 2.16 ние имаме:

Използвайки формули (2.1) и (2.5), намираме съответно статичния момент на полукръга около оста 0 (x ( и ординатата в 0 центъра на тежестта ОТНОСНО в координатна система 0 (x (yy

Относно осите 0, x и 0 (y v които са основните оси за полукръга, аксиалните моменти на инерция са равни на половината инерционни моменти на окръжността:

Моментът на инерция около главната централна ос се определя с помощта на първата формула (2.6):

Елипса.За изчисляване на аксиалния момент на инерция на елипса с полуоси и и б около оста О (Фиг. 2.17) ще продължим по следния начин. Ще опишем кръг около елипсата и ще изберем две елементарни ленти с ширина dx и височина 2y до за кръг и 2 ъъъ за елипса. Моментите на инерция на тези две ленти могат да бъдат определени от първата от формулите (2.15) за правоъгълник:

Чрез интегриране на тези изрази, вариращи от -и преди и, вземете

Фигура: 2.16

Фигура: 2.17

От уравненията на окръжността и елипсата имаме

Имайки това предвид

Подобен израз може да се получи за момента на инерцията около оста OU. В резултат на това за елипсата ще имаме следните формули за аксиалните моменти:

Подвижни пръти.Геометричните характеристики на участъците от валцувани пръти (двустранни греди, канали, ъгли) са дадени в таблиците на асортимента от валцувана стомана (вж. Приложението).

Аксиалният (или екваториален) момент на инерция на даден участък спрямо определена ос е сумата от произведенията на елементарни площи на квадратите на техните разстояния от тази ос, взети по цялата му площ F, т.е.

Полярният момент на инерция на един участък спрямо точка (полюс) е сумата от произведенията на елементарни площи по квадратите на техните разстояния от тази точка, взети по цялата му площ F, т.е.

Центробежният инерционен момент на даден участък спрямо някои две взаимно перпендикулярни оси е сумата от произведенията на елементарни площи, взети върху цялата му площ F от техните разстояния от тези оси, т.е.

Моментите на инерция се изразяват в и т.н.

Аксиалните и полярните моменти на инерция винаги са положителни, тъй като техните изрази под интегралните знаци включват стойностите на площите (винаги положителни) и квадратите на разстоянията на тези области от дадена ос или полюс.

На фиг. 9.5, а показва разрез с площ F и показва оста y и z. Аксиални моменти на инерция на този участък спрямо осите y:

Сборът от тези моменти на инерция

и следователно

По този начин сумата от аксиалните моменти на инерция на участъка спрямо две взаимно перпендикулярни оси е равна на полярния момент на инерция на този участък спрямо точката на пресичане на тези оси.

Центробежните моменти на инерция могат да бъдат положителни, отрицателни или нулеви. Така например, центробежният инерционен момент на участъка, показан на фиг. 9.5, a, спрямо осите y и е положителен, тъй като за основната част на този раздел, разположен в първия квадрант, стойностите и следователно са положителни.

Ако промените положителната посока на оста y или обратното (Фигура 9.5, b) или завъртите двете оси на 90 ° (Фигура 9.5, c), тогава центробежният инерционен момент ще стане отрицателен (неговата абсолютна стойност ще не се променя), тъй като основната част на секцията ще бъде разположена в квадрант, за който координатите y са положителни, а координатите z отрицателни. Ако промените положителните посоки на двете оси в противоположни, това няма да промени нито знака, нито величината на центробежния инерционен момент.

Помислете за фигура, която е симетрична на една или повече оси (Фигура 10.5). Нека нарисуваме осите, така че поне една от тях (в този случай оста y) да съвпада с оста на симетрия на фигурата. Всяко място, разположено вдясно от оста, съответства в този случай на същото място, разположено симетрично на първото, но вляво от оста y. Центробежният инерционен момент на всяка двойка от такива симетрично разположени области е:

Следователно,

По този начин центробежният инерционен момент на участъка около осите, от които едната или и двете съвпадат с нейните оси на симетрия, е нула.

Аксиалният момент на инерция на сложен участък спрямо определена ос е равен на сумата от аксиалните моменти на инерция на съставните му части спрямо същата ос.

По подобен начин центробежният инерционен момент на сложен участък спрямо всякакви две взаимно перпендикулярни оси е равен на сумата от центробежните моменти на инерция на съставните му части спрямо същите оси. Също така, полярният момент на инерция на сложен участък спрямо някаква точка е равен на сумата от полярните моменти на инерция на съставните му части спрямо същата точка.

Имайте предвид, че инерционните моменти, изчислени за различни оси и точки, не могат да се събират.

05-12-2012: Адолф Сталин

Би било хубаво да обясня с визуален пример за особено надарени хора като мен какъв е моментът на инерция и с какво се яде. На специализирани сайтове всичко е някак много объркващо и Doc има ясен талант да предава информация, може би не най-трудната, но много компетентна и разбираема

05-12-2012: Д-р Лом

По принцип какъв е моментът на инерция и откъде е дошъл е обяснено достатъчно подробно в статията „Основи на якостните материали, формули за проектиране“, тук само ще повторя: „W е моментът на съпротивление на напречното сечение на гредата, с други думи, площта на свиваемата или опъната част от напречното сечение на гредата, умножена по рамото на действието на получената сила. " Моментът на съпротивление трябва да бъде известен за изчисления на якостта на конструкцията, т.е. чрез ограничаване на напреженията. Моментът на инерция трябва да бъде известен, за да се определят ъглите на въртене на напречното сечение и деформацията (изместването) на центъра на тежестта на напречното сечение, тъй като максималните деформации се появяват в най-горния и в най-долния слой на огънатата конструкция , тогава моментът на инерция може да се определи чрез умножаване на момента на съпротивлението по разстоянието от секциите на центъра на тежестта до горния или долния слой, следователно за правоъгълни участъци I \u003d Wh / 2. Когато се определя моментът на инерция на участъци от сложни геометрични фигури, първо сложната фигура се разделя на прости, след това се определят областите на напречното сечение на тези фигури и инерционните моменти на най-простите фигури, след това площите на най-простите фигурите се умножават по квадрата на разстоянието от общия център на тежестта на участъка до центъра на тежестта на най-простата фигура. Моментът на инерция на най-простата фигура в сложен участък е равен на момента на инерция на фигурата + квадратът на разстоянието, умножен по площта. След това получените моменти на инерция се сумират и се получава моментът на инерция на сложен участък. Но това са най-опростените формулировки (въпреки че, съгласен съм, все още изглежда доста сложно). След време ще напиша отделна статия.

20-04-2013: Петър

Не е нужно да се доверявате напълно на информацията, предоставена на сайтовете. Никой не я проверява по приятелски начин. И връзки към него не се дават. И така, в Таблица 1. „Форми на сечение, площи на напречното сечение, моменти на инерция и моменти на съпротивление за конструкции с достатъчно прости геометрични форми“ за тънкостенна тръба се определя, че съотношението на диаметъра към дебелината на черупката трябва да е повече от 10. Според други източници трябва да е повече от 20! !! (Н. М. Беляев. Якост на материалите. М.1996. С.160. Или Н. И. Безухов. Основи на теорията на еластичността, пластичността и пълзенето. М.1961. С.390)

21-04-2013: Д-р Лом

Нали. Не можете да се доверите. Но логическото мислене все още не е отменено. Най-правилният вариант е да се изчисли моментът на инерция или моментът на съпротивление за всяка тръба, като се използват формулите, дадени за конвенционална тръба (с 1 точка по-висока). Формулите, дадени за тънкостенна тръба, във всеки случай ще бъдат приблизителни и са подходящи само за първоначалното изчисление и това не трябва да се забравя.
Параметрите на максимално допустимата дебелина на стената обаче бяха коригирани.

25-06-2013: Саня

изисква се да се определи моментът на инерция за сложен нестандартен участък. разрез: правоъгълник с два канала. изглежда като буквата "W". Не мога да намеря никаква информация. Ще съм благодарен за малко информация

25-06-2013: Д-р Лом

Погледнете статията "Изчисляване на якостта на таванния профил за гипсокартон" (http: //site/item249.html)
там, по-специално, моментът на инерция също се определя от не съвсем прост участък.

04-11-2014: Д-р Лом

Формулата от източника, който сте предоставили, е неправилна (може да се използва само за приблизителни изчисления) и е лесно да я проверите.
За да се определи моментът на инерция на тръбната секция, е достатъчно да се извади моментът на инерция на отвора (вътрешен диаметър, тъй като вътре в тръбата няма материал, поради което е тръба) от момента на инерцията на кръгла лента (тук при изчисленията се използва външният диаметър на тръбата). След най-простите математически преобразувания получаваме формулата за момента на инерцията на тръбата, дадена в таблицата.
И за да се определи моментът на съпротивление, моментът на инерция трябва да бъде разделен на максималното разстояние от центъра на тежестта до най-отдалечената точка на участъка, съответно по D / 2, или умножено по 2 / D.
В резултат на това е невъзможно да получите формулата, която сте посочили, и колкото по-дебела е стената на тръбата, толкова по-голяма е грешката при използването на тази формула.

04-11-2014: Радик

Благодаря док!

11-11-2014: Илгам

Не можах да намеря информация за мерните единици, в които (mm, cm, m) всички стойности във формулите.
Опитах се да изчисля Wz за ъгъл от 210x90mm (ако горният рафт е отрязан на канала 24P), се оказа 667,5 cm3, при условие че всички стойности са в cm.
Например за 24P канал (преди рязане на фланеца) Wx (Wz) \u003d 243 cm3.

11-11-2014: Д-р Лом

Това са общи формули. В какви единици заместват стойностите, в такива и получават резултата, само разбира се вече в кубични. Но ако те започнат да се заменят, например, в сантиметри, тогава ето как трябва да продължите.
За канал без фланец моментът на съпротивление по подразбиране не може да бъде по-голям от този на цял канал. За приблизително определяне на момента на съпротивление на канал без фланец, можете да използвате формулите за неравен ъгъл (само за определяне на Wz, тези формули няма да работят за Wy).

04-01-2015: Валерий

Ако участъкът на тръбата е отслабен от няколко значителни отвора, как това може да се вземе предвид при изчисляване на момента на инерцията и момента на съпротивлението? Тръба 32,39 см и 9 дупки в нея. диаметър 2.8 см в напречно сечение (стъпка на отвора 10 см по дължината на тръбата).

05-01-2015: Д-р Лом

За да определите момента на инерцията, трябва да извадите момента на инерция на вашата дупка от момента на инерцията на тръбата. За да направите това, трябва да определите площта на напречното сечение на отвора и след това да го умножите по квадрата на разстоянието до центъра на тръбата плюс вътрешния момент на инерция на отвора. Повече подробности в статията "Моменти на инерция на напречните сечения".
Ако изчислението не изисква специална точност и диаметърът на отвора е 5 или повече пъти по-малък от диаметъра на тръбата (като вашия случай, ако 32,39 е външният диаметър), тогава отворът може да бъде намален до правоъгълник. Ако отворът не е през, тогава допълнително трябва да определите позицията на центъра на тежестта на тръбата с отвора, за да изчислите новата стойност на момента на съпротивление.
Но това не е всичко. Трябва да вземете предвид, че в близост до дупките възникват значителни локални напрежения.

09-10-2015: Борис

Неравен ъгъл. Когато се изчислява Wy, не y, а H-y

09-10-2015: Д-р Лом

Не разбирам какво имаш предвид. Определението на момента на съпротивление около оста y не е дадено в таблиците изобщо.

09-10-2015: Борс

За триъгълници, при изчисляване на Wzп h на квадрат.

09-10-2015: Борис

09-10-2015: Д-р Лом

Всичко е правилно. Сега разбирам какво имаш предвид. По-правилно би било да посочите момента на съпротивление за горната и долната част на секцията, а аз посочих само за долната. Е, когато се определя моментът на съпротивление на триъгълниците, квадратът банално се пропуска.
Поправено. Благодаря за вниманието.

28-04-2016: Джама

Здравейте! Кой може да помогне за коректността на изчислението http://ej.kubagro.ru/2011/02/pdf/19.pdf
Не мога да разбера откъде идва моментът на съпротива. Помогнете ми моля! 21-03-2017: игор

здравей Сергей. Прочетох някои от вашите статии, много интересни и разбираеми (най-вече). Бих искал да изчисля I-лъч, но не мога да намеря Ix и Wx. факт е, че не е стандартен, ще го направя сам от дърво.можете ли да ми помогнете? Ще плащам. Само аз не мога да плащам по електронен път. Не знам как да го използвам.

21-03-2017: Д-р Лом

Игор, изпратих ти писмо.

30-08-2017: Али

Скъпи докторе, пожелавам ви всичко най-добро. Моля, помогнете ми с какви формули са необходими за избор и проверка на якостта на лъча от следните секции: Канал, ъгъл и профил на крушката, имащ допустим момент на съпротивление W \u003d 58,58 cm3. много благодаря и очаквам с нетърпение вашата помощ.

31-08-2017: Д-р Лом

Вижте статията "Изчисляване на стоманени еднопролетни греди с шарнирни опори при огъване съгласно SP 16.13330.2011", всичко е описано достатъчно подробно там.

13-11-2017: Абдуахад

Здравейте, моля, кажете ми защо Ql ^ 2/8 защо се дели на 8 и защо понякога делим на 6 и 24 и т.н., моля, кажете ми, просто не разбрах