Modi di base per affrontare lo stress
Da questo articolo imparerai: Cosa può essere uno stress pericoloso e perché è così importante affrontarlo Quali sono i modi ...
Il momento d'inerzia assiale è la somma, presa sull'intera sezione, dei prodotti delle aree elementari per il quadrato della distanza da un asse giacente nel piano della sezione considerata. Il momento d'inerzia assiale è una misura della capacità della trave di resistere alla deformazione flessionale.
J - Momento d'inerzia assiale
J x = 
J y = 
Momento di resistenza assiale chiamato atteggiamento momento assiale inerzia alla distanza dalle fibre della sezione più lontana dall'asse neutro.
W - Momento assiale di resistenza.
W x =, W y =
Momento d'inerzia polare si chiama, presa su tutta la sezione, la somma dei prodotti delle aree elementari per i quadrati delle loro distanze dal baricentro della sezione, cioè prima dell'intersezione degli assi coordinati.
Il momento d'inerzia polare caratterizza la capacità di una parte di resistere alla deformazione torsionale.
Momento d'inerzia polare.
= .
.
Momento di resistenza polare detto rapporto tra il momento d'inerzia polare e la distanza dei punti più distanti della sezione dal baricentro della sezione considerata.
Momento di resistenza polare
1. Sezione rettangolare.

J y = (mm 4), J x = (mm 4)
W x =  (mm 3), W y =
(mm 3), W y =  (millimetro 3)
(millimetro 3)
2. Sezione tonda

J x = J y = (mm 4), = (mm 4)
W y = W x =  (mm3), =
(mm3), =  (millimetro 3)
(millimetro 3)
3. Sezione anulare

J x = J y = - =  (mm 4), α = d / D
(mm 4), α = d / D
W y = W x =  (millimetro 3)
(millimetro 3)
= 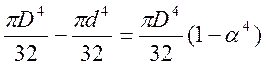 (millimetro 4)
(millimetro 4)
= (millimetro 3)
(millimetro 3)
4. Sezione scatola.

J x =  =
= (millimetro 4)
(millimetro 4)
J y =  =
= (millimetro 4)
(millimetro 4)
W x =  (millimetro 3)
(millimetro 3)
W y =  (millimetro 3)
(millimetro 3)
Calcolo di parti con distribuzione uniforme delle sollecitazioni.
Questo tipo di parti include aste con alette e perni, nonché cilindri idraulici e pneumatici e altri recipienti a pressione, elementi bimetallici (relè termici).
Calcolo della spinta.

1) Forza di trazione F applicata all'asta.
L'asta prende un carico longitudinale, sotto l'azione del quale si allunga. In questo caso, l'entità dell'allungamento assoluto è determinata dalla legge di Hooke espansa:
σ p = Eε. , р = F / A,  , р = F / A<=[
σ р ]= σ T / n -
, р = F / A<=[
σ р ]= σ T / n -
condizione di resistenza alla trazione, (A = H * B, A =).
Le alette, a seguito dell'interazione con il dito, vengono schiacciate sull'area di contatto.
Condizione di resistenza al collasso:
cm = F / LA<=[σ см ]= 2σ T / n , A=d*b.
Le dita sono calcolate per un taglio dall'interazione con le alette:
τ cf = F / A<=[τ ср ]= 0,5σ T / n; A=*i, i - количество платежей среза (i=2).
2) Alla spinta viene applicata una forza di compressione F2.
L'asta è in compressione. L'entità dell'accorciamento assoluto è determinata allo stesso modo secondo la legge di Hooke:
c = F / LA<=[σ с ]=[σ р ]=σ T / n. – Для коротких стержней тяги.
Asta lunga - quando la lunghezza è 3 volte una delle dimensioni della sezione trasversale. Qui c'è una possibilità di flessione istantanea dell'asta di spinta.
с =<=[σ с ]=[σ р ]=σ T / n, φ – коэффициент продольного изгиба, величина табличная – зависит от материала, гибкости стержня и характера закрепления концов стержня.
L'occhiello e le dita vengono calcolati allo stesso modo del calcolo precedente.
Calcolo dei vasi a parete sottile.
Le navi a parete sottile includono cilindri idraulici e pneumatici, ricevitori, condutture, ecc.
A seconda della forma, i vasi sono:
cilindrico (cilindri idraulici e pneumatici, alcuni tipi di ricevitori, tubazioni);
palla (alcuni tipi di ricevitori, fondi e coperchi di vasi cilindrici, membrane, ecc.);
toro (tratti curvi di tubazioni, elementi sensibili di comparatori).
In tutte le navi, sotto l'azione delle forze interne di un liquido o di un gas, si verificano sollecitazioni nelle pareti nelle sezioni longitudinali e trasversali.
Vasi cilindrici.
 Un sottile guscio cilindrico viene caricato con una pressione interna P. - Calcolato come sezione trasversale di un cilindro.
Un sottile guscio cilindrico viene caricato con una pressione interna P. - Calcolato come sezione trasversale di un cilindro.
Tore navi.
Sono calcolati come cilindrici curvi.
15.10.04 Calcolo delle sollecitazioni derivanti dalle variazioni di temperatura.

Con le fluttuazioni di temperatura, una parte fissata tra supporti rigidi subisce una deformazione per compressione o tensione. Quando la temperatura aumenta (diminuisce) di Dt, l'asta dovrebbe allungarsi (accorciarsi) della quantità di allungamento assoluto (accorciarsi):
Dio= unT* io* DT, dove a t è il coefficiente di temperatura dell'espansione lineare (per acciaio 12 * 10 -6 ° С -1), quindi il valore di allungamento assoluto (accorciamento): Δε t = Δ l t / io = α t* DT, ma dal momento che l'asta è fissata rigidamente, quindi non può allungarsi (accorciarsi), quindi nel suo materiale sorgeranno sollecitazioni di compressione (trazione), i cui valori sono determinati dalla legge di Hooke:
с, р = Е * ε t = E * α t * Δt.
Nella pratica computazionale, le sezioni si trovano spesso nella forma delle forme più semplici (rettangoli, cerchi, triangoli, ecc.) o nelle loro combinazioni. Quando si calcolano i momenti di inerzia di tali figure, vengono solitamente utilizzate formule di calcolo predefinite. Diamo un'occhiata ad alcune delle forme.
Rettangolo e parallelogramma (Fig. 6.4). Selezioniamo una striscia elementare con un'area dF= bdy e sostituisci questo valore dF sotto il segno di integrale (6.5):
I momenti di inerzia di queste figure rispetto agli assi passanti per la base si ricavano dalla formula (6.13):
|
|
Momenti d'inerzia di un rettangolo attorno agli assi sìC e sì sono calcolati dalle formule (6.16) e (6.17), dove Bè sostituito da h, un h Su B:
Calcolando il momento d'inerzia del triangolo attorno all'asse centrale parallelo alla base mediante le formule di trasferimento, si ottiene

Solitamente le dimensioni della sezione circolare sono espresse in termini di diametro D e contare ioP secondo la formula
Assi centrali sì e z dividere il cerchio in quattro parti completamente identiche con uguali momenti di inerzia attorno a questi assi. Di conseguenza, i momenti di inerzia di un cerchio e un semicerchio attorno agli assi sì e z dovrebbe essere pari, rispettivamente, a quadruplicare e raddoppiare i momenti di inerzia relativi agli stessi assi di un quarto di cerchio. Da quanto detto segue che i momenti di inerzia del semicerchio attorno all'asse di simmetria sì e assi z, passante per la sua base (Fig. 6.2), sarà uguale e pari alla metà del momento d'inerzia del cerchio,
e i momenti di inerzia di un quarto di cerchio
Per sezioni semplici, i momenti statici ei momenti di inerzia si trovano dalle formule (2.1) - (2.4) utilizzando l'integrazione. Si consideri, ad esempio, il calcolo del momento di inerzia assiale J x per una sezione arbitraria mostrata in Fig. 2.9. Considerando che in un sistema di coordinate rettangolari l'elemento area dF = dxdy, ottenere
dove indice ^ (y) e x in (y) - coordinate dei punti del contorno ad un valore fisso a.
Integrando su x, troviamo

La quantità Di)è la larghezza della sezione al livello a(vedi Fig. 2.9) e il prodotto b (y) dy = dF - area della striscia elementare ombreggiata parallela all'asse Oh. Con questo in mente, la formula per / viene convertita nella forma

Analoga espressione si ottiene per il momento d'inerzia J y.
Rettangolo. Troviamo i momenti d'inerzia attorno agli assi centrali principali, che, in accordo con la proprietà 2 (§ 2.5), coincidono con gli assi di simmetria del rettangolo (Fig. 2.10). Poiché la larghezza della sezione è costante, allora per la formula (2.14) si ottiene

Momento d'inerzia attorno all'asse Oh x x x definiamo con la prima delle formule (2.6): 


Momenti di inerzia / e J si trovano in modo simile. Scriviamo le formule per i momenti di inerzia assiale del rettangolo:
Triangolo arbitrario. Innanzitutto, troviamo il momento d'inerzia attorno all'asse 0 (x v passante per la base del triangolo (Fig. 2.11). Larghezza della sezione Di () a livello a ( si trova dalla somiglianza dei triangoli:

Sostituendo questa quantità nella formula (2.14) ed effettuando l'integrazione, si ottiene

Momenti relativi agli assi Oh e 0 2 x 2, parallela alla base e passante rispettivamente per il baricentro e per l'apice del triangolo, troviamo utilizzando le formule (2.6):

In queste formule b (= h / 3 e b2 = -2h/ 3 - rispettivamente, le ordinate del baricentro del triangolo oh nel sistema di coordinate Oh x x 1 y 1 e 0 2 x 2 e t


1 ° 2 р * аУ 1
TL P * 2
r> 4 ™ _ ° 2 1
Д__V _! _ * _ / ^ * 3
V xv *; -7 ^ Am ^
U_ U-_XI - UZ__y
Oh,| B *, 0 Si/Si 2 %*1
Riso. 2.11 Riso. 2.12
Scriviamo le formule per i momenti di inerzia assiale del triangolo attorno agli assi paralleli alla base:
Triangoli rettangolari e isosceli. Per un triangolo rettangolo (Fig. 2.12) definiamo il momento d'inerzia centrifugo J sugli assi centrali Oh e UO, parallela alle gambe. Questo può essere fatto usando la formula (2.3). Tuttavia, la soluzione al problema può essere semplificata applicando la seguente tecnica. Usando la mediana 0 { 0 3 dividere il triangolo dato in due triangoli isosceli 0 (0 3 A e Ofi 3 B. Assi 0 3 x 3 e 0 3 e 3 sono gli assi di simmetria per questi triangoli e in base alla proprietà 2 (§ 2.5) saranno gli assi principali di ciascuno di essi separatamente, e quindi dell'intero triangolo Oh x AB. Pertanto, il momento d'inerzia centrifugo J= 0. Centrifuga
momento del triangolo attorno agli assi Oh e OU troviamo usando l'ultima delle formule (2.6):
Scriviamo le formule per i momenti di inerzia di un triangolo rettangolo: 



Il momento d'inerzia di un triangolo isoscele attorno all'asse di simmetria OU(Fig. 2.13) definiamo, utilizzando la quarta delle formule (2.17), il momento d'inerzia raddoppiato di un triangolo rettangolo con base h e altezza B / 2:

Quindi, i momenti di inerzia di un triangolo isoscele attorno ai principali assi centrali Oh e OU sono determinati dalle formule
Cerchio. All'inizio, è conveniente calcolare il momento d'inerzia polare di un cerchio con la formula (2.4), usando il sistema di coordinate polari (Fig. 2.14).
Considerando che dF-rdrdQ, trova

Poiché il momento polare secondo (2.4) è uguale alla somma di due momenti assiali, si ottiene
Squillo. I momenti di inerzia dell'anello (Fig. 2.15) si trovano come differenza tra i momenti di inerzia di due cerchi con raggi io sono 2 e R (:
Semicerchio(Riso. 2.16). Seleziona l'elemento dell'area nel piano del semicerchio dF con coordinate polari G, 0 e coordinate cartesiane x v y v per cui, secondo la Fig. 2.16 noi abbiamo:
Usando le formule (2.1) e (2.5), troviamo, rispettivamente, il momento statico del semicerchio attorno all'asse 0 (x ( e l'ordinata a 0 del baricentro oh nel sistema di coordinate 0 (x (yy

Rispetto agli assi 0, x e 0 (y v quali sono gli assi principali del semicerchio, i momenti di inerzia assiali sono pari alla metà dei momenti di inerzia del cerchio:

Il momento d'inerzia attorno all'asse centrale principale è determinato utilizzando la prima formula (2.6):
Ellisse. Per calcolare il momento d'inerzia assiale di un'ellisse con semiassi un e B intorno all'asse Oh(Fig. 2.17) procederemo come segue. Descriveremo un cerchio attorno all'ellisse e selezioneremo due strisce elementari con una larghezza dx e altezza 2 anni a per cerchio e 2 uh per un'ellisse. I momenti di inerzia di queste due bande possono essere determinati dalla prima delle formule (2.15) per un rettangolo:
Integrando queste espressioni che vanno da -un prima un, ottenere 

Riso. 2.16

Riso. 2.17
Dalle equazioni del cerchio e dell'ellisse si ha

Con questo in testa

Un'espressione simile si può ottenere per il momento d'inerzia attorno all'asse UO. Di conseguenza, per l'ellisse avremo le seguenti formule per i momenti assiali:
Canne di rotolamento. Le caratteristiche geometriche delle sezioni delle barre laminate (travi a I, canali, angoli) sono riportate nelle tabelle dell'assortimento di laminati (vedi appendice).
Il momento d'inerzia assiale (o equatoriale) di una sezione attorno a un certo asse è la somma dei prodotti delle aree elementari per i quadrati delle loro distanze da questo asse preso su tutta la sua area F, cioè
![]()
Il momento d'inerzia polare di una sezione rispetto a un punto (polo) è la somma dei prodotti delle aree elementari per i quadrati delle loro distanze da questo punto presa su tutta la sua area F, cioè
![]()
Il momento d'inerzia centrifugo della sezione rispetto a circa due assi reciprocamente perpendicolari è la somma dei prodotti delle aree elementari prese su tutta la sua area F per le loro distanze da questi assi, cioè
![]()
I momenti di inerzia sono espressi in, ecc.
I momenti di inerzia assiale e polare sono sempre positivi, poiché le loro espressioni sotto i segni di integrale includono i valori delle aree (sempre positivi) e i quadrati delle distanze di queste aree da un dato asse o polo.

Nella fig. 9.5, a mostra una sezione con un'area F e mostra gli assi yez. Momenti di inerzia assiali di questa sezione rispetto agli assi y:
![]()
La somma di questi momenti di inerzia
e quindi
![]()
![]()
Pertanto, la somma dei momenti di inerzia assiale della sezione rispetto a due assi reciprocamente perpendicolari è uguale al momento di inerzia polare di questa sezione rispetto al punto di intersezione di questi assi.
I momenti di inerzia centrifuga possono essere positivi, negativi o nulli. Quindi, ad esempio, il momento d'inerzia centrifugo della sezione mostrata in Fig. 9.5, a, relativo all'asse y ed è positivo, poiché per la parte principale di questa sezione, situata nel primo quadrante, i valori, e quindi, sono positivi.
Se si cambia la direzione positiva dell'asse y o quella opposta (Figura 9.5, b) o si ruotano entrambi questi assi di 90 ° (Figura 9.5, c), il momento d'inerzia centrifugo diventerà negativo (il suo valore assoluto sarà non cambia), poiché la parte principale la sezione sarà quindi situata in un quadrante per cui le coordinate y sono positive e le coordinate z sono negative. Se si modificano le direzioni positive di entrambi gli assi in senso opposto, ciò non cambierà né il segno né l'entità del momento d'inerzia centrifugo.

Consideriamo una figura simmetrica rispetto a uno o più assi (Figura 10.5). Disegniamo gli assi in modo che almeno uno di essi (in questo caso, l'asse y) coincida con l'asse di simmetria della figura. In questo caso, ogni sito situato a destra dell'asse corrisponde allo stesso sito situato simmetricamente al primo, ma a sinistra dell'asse y. Il momento d'inerzia centrifugo di ciascuna coppia di tali piattaforme disposte simmetricamente è pari a:
Quindi,
Pertanto, il momento d'inerzia centrifugo della sezione attorno agli assi, di cui uno o entrambi coincidono con i suoi assi di simmetria, è uguale a zero.
Il momento d'inerzia assiale di una sezione complessa rispetto ad un certo asse è uguale alla somma dei momenti d'inerzia assiale delle sue parti costituenti rispetto allo stesso asse.
Allo stesso modo, il momento d'inerzia centrifugo di una sezione complessa rispetto a due assi reciprocamente perpendicolari è uguale alla somma dei momenti d'inerzia centrifughi delle sue parti costituenti rispetto agli stessi assi. Inoltre, il momento d'inerzia polare di una sezione complessa rispetto a un certo punto è uguale alla somma dei momenti d'inerzia polare delle sue parti costituenti rispetto allo stesso punto.
Si noti che i momenti di inerzia calcolati rispetto a diversi assi e punti non possono essere sommati.

05-12-2012: Adolf Stalin
Sarebbe bello spiegare con un esempio visivo per persone particolarmente dotate, come me, cos'è il momento di inerzia e con cosa si mangia. Sui siti specializzati, tutto è in qualche modo molto confuso e Doc ha un chiaro talento nel trasmettere informazioni, forse non il più complicato, ma molto competente e chiaro
05-12-2012: Dott. Lomé
In linea di principio, qual è il momento di inerzia e da dove viene è spiegato in modo sufficientemente dettagliato nell'articolo "Fondamenti dei materiali di resistenza, formule di progettazione", qui ripeterò solo: "W è il momento di resistenza della sezione trasversale della trave, in altre parole, l'area della parte comprimibile o stirata della sezione trasversale della trave, moltiplicata per la spalla dell'azione della forza risultante. " Il momento di resistenza deve essere noto per i calcoli di resistenza della struttura, ad es. limitando le sollecitazioni. Il momento d'inerzia deve essere noto per determinare gli angoli di rotazione della sezione trasversale e la deflessione (spostamento) del baricentro della sezione trasversale, poiché le deformazioni massime si verificano nello strato superiore e inferiore della struttura piegata , allora il momento d'inerzia può essere determinato moltiplicando il momento resistente per la distanza dalle sezioni del baricentro allo strato superiore o inferiore, quindi per sezioni rettangolari I = Wh / 2. Quando si determina il momento di inerzia di sezioni di forme geometriche complesse, prima una figura complessa viene suddivisa nella più semplice, quindi vengono determinate le aree della sezione trasversale di queste figure e i momenti di inerzia delle figure più semplici, quindi le aree delle più semplici le figure vengono moltiplicate per il quadrato della distanza dal baricentro generale della sezione al baricentro della figura più semplice. Il momento d'inerzia della figura più semplice in una sezione complessa è uguale al momento d'inerzia della figura + il quadrato della distanza moltiplicato per l'area. Quindi si sommano i momenti di inerzia ottenuti e si ottiene il momento di inerzia di una sezione complessa. Ma queste sono le formulazioni più semplificate (anche se, sono d'accordo, sembra ancora piuttosto complicato). Nel tempo, scriverò un articolo separato.
20-04-2013: Petr
Non è necessario fidarsi completamente delle informazioni fornite sui siti. Nessuno lo controlla in modo amichevole. E i collegamenti ad esso non sono forniti. Quindi nella Tabella 1. "Forme in sezione, aree di sezione, momenti di inerzia e momenti di resistenza per strutture di forme geometriche abbastanza semplici" per un tubo a parete sottile, si determina che il rapporto tra il diametro e lo spessore del guscio dovrebbe essere maggiore di 10. Secondo altre fonti, dovrebbe essere più di 20!!! (NM Belyaev. Resistenza dei materiali. M.1996. P.160. O NI Bezukhov. Fondamenti della teoria dell'elasticità, plasticità e scorrimento. M.1961.p.390)
21-04-2013: Dott. Lomé
Destra. Non puoi fidarti. Ma il pensiero logico non è stato ancora cancellato. L'opzione più corretta è calcolare il momento d'inerzia o il momento resistente per qualsiasi tubo utilizzando le formule fornite per un tubo convenzionale (1 punto più alto). Le formule fornite per un tubo a parete sottile, in ogni caso, saranno approssimative e adatte solo per il calcolo iniziale, e questo non dovrebbe essere dimenticato.
Tuttavia, i parametri dello spessore massimo consentito della parete sono stati corretti.
25-06-2013: Sanya
è necessario determinare il momento d'inerzia per una sezione complessa non standard. sezione: rettangolo con due scanalature. assomiglia alla lettera "W". Non riesco a trovare alcuna informazione. Sarò grato per alcune informazioni
25-06-2013: Dott. Lomé
Guarda l'articolo "Calcolo della resistenza del profilo del soffitto per cartongesso" (http: //site/item249.html)
lì, in particolare, è determinato anche il momento d'inerzia di una sezione non del tutto semplice.
04-11-2014: Dott. Lomé
La formula della fonte che hai fornito non è corretta (può essere utilizzata solo per calcoli approssimativi) ed è facile verificarla.
Per determinare il momento d'inerzia della sezione del tubo è sufficiente sottrarre il momento d'inerzia del foro (diametro interno, perché non c'è materiale all'interno del tubo, ecco perché è un tubo) dal momento d'inerzia di una barra circolare (qui nei calcoli viene utilizzato il diametro esterno del tubo). Dopo le più semplici trasformazioni matematiche, otteniamo la formula per il momento d'inerzia del tubo, riportato nella tabella.
E per determinare il momento di resistenza, il momento di inerzia deve essere diviso per la distanza massima dal centro di gravità al punto più lontano della sezione, rispettivamente, per D / 2 o moltiplicato per 2 / D.
Di conseguenza, è impossibile ottenere la formula specificata e più spessa è la parete del tubo, maggiore è l'errore quando si utilizza questa formula.
04-11-2014: Radik
Grazie dottore!
11-11-2014: Ilgami
Non sono riuscito a trovare informazioni sulle unità in cui (mm, cm, m) tutti i valori nelle formule.
Ho provato a calcolare Wz per un angolo di 210x90mm (se il ripiano superiore è tagliato nel canale 24P), è risultato 667,5 cm3, a condizione che tutti i valori siano in cm.
Ad esempio, per il canale 24P (prima del taglio della flangia) Wx (Wz) = 243 cm3.
11-11-2014: Dott. Lomé
Queste sono formule generali. In quali unità sostituire i valori, in tale e ottenere il risultato, solo ovviamente già in quelli cubici. Ma se hanno iniziato a sostituire, ad esempio, in centimetri, allora è così che devi continuare.
Per un canale senza flangia, il momento di resistenza predefinito non può essere maggiore di quello di un intero canale. Per una determinazione approssimativa del momento di resistenza di un canale senza flangia, è possibile utilizzare le formule per un angolo disuguale (solo per determinare Wz, queste formule non funzioneranno per Wy).
04-01-2015: Valerij
Se la sezione del tubo è indebolita da diversi fori significativi, come si può tenerne conto nel calcolo del momento d'inerzia e del momento resistente? Tubo di 32,39 cm e 9 fori. diam.2,8 cm di sezione (passo dei fori 10 cm. lungo la lunghezza del tubo).
05-01-2015: Dott. Lomé
Per determinare il momento d'inerzia, devi sottrarre il momento d'inerzia del tuo foro dal momento d'inerzia del tubo. Per fare ciò, è necessario determinare l'area della sezione trasversale del foro e quindi moltiplicarla per il quadrato della distanza dal centro del tubo più il momento d'inerzia intrinseco del foro. Maggiori dettagli nell'articolo "Momenti di inerzia delle sezioni trasversali".
Se il calcolo non richiede una precisione particolare e il diametro del foro è 5 o più volte più piccolo del diametro del tubo (come nel tuo caso, se 32,39 è il diametro esterno), il segmento del foro può essere ridotto a un rettangolo. Se il foro non è passante, è necessario determinare ulteriormente la posizione del baricentro del tubo con il foro per calcolare quindi il nuovo valore del momento resistente.
Ma non è tutto. È necessario tenere conto del fatto che in prossimità dei fori si verificano notevoli sollecitazioni locali.
09-10-2015: Boris
Angolo disuguale Quando si calcola Wy, non y, ma H-y
09-10-2015: Dott. Lomé
Non capisco cosa intendi. La definizione del momento resistente rispetto all'asse y non è data affatto nelle tabelle.
09-10-2015: Bors
Per i triangoli nel calcolo di Wzп h al quadrato.
09-10-2015: Boris
09-10-2015: Dott. Lomé
Tutto è corretto. Adesso ho capito cosa intendi. Sarebbe più corretto indicare il momento di resistenza per la parte superiore e inferiore della sezione, e ho indicato solo per quella inferiore. Bene, quando si determina il momento di resistenza dei triangoli, il quadrato è banalmente mancato.
corretto. Grazie per l'attenzione.
28-04-2016: Jama
Ciao! Chi può aiutare sulla correttezza del calcolo http://ej.kubagro.ru/2011/02/pdf/19.pdf
Non riesco a capire da dove provenga il momento della resistenza. Aiutami per favore! 21-03-2017: Igor
ciao Sergey. Ho letto alcuni tuoi articoli, molto interessanti e comprensibili (soprattutto).Vorrei calcolare un I-beam ma non riesco a trovare Ix e Wx. il fatto è che non è standard, lo farò io stesso, in legno, puoi aiutarmi? Pagherò Solo io non sarò in grado di pagare con mezzi elettronici. Non so come usarlo.
21-03-2017: Dott. Lomé
Igor, ti ho mandato una lettera.
30-08-2017: Ali
Gentile dottore, le auguro ogni bene. Per favore aiutami con quali formule sono necessarie per selezionare e verificare la forza del raggio delle seguenti sezioni: profilo del canale, dell'angolo e del bulbo, con un momento di resistenza ammissibile W = 58,58 cm3. grazie mille e attendo un vostro aiuto.
31-08-2017: Dott. Lomé
Guarda l'articolo "Calcolo delle travi a campata singola in acciaio con supporti incernierati in flessione secondo SP 16.13330.2011", tutto è descritto in modo sufficientemente dettagliato lì.
13-11-2017: Abduahad
Ciao, per favore dimmi perché Ql ^ 2/8 perché è diviso per 8 e perché a volte dividiamo per 6 e 24, ecc., per favore dimmi, non ho capito